Speichern eines int - Wertes

Wertebereich

Variablen vom Typ int belegen einen Speicherplatz von 4 Byte. Das sind 32 Bit. Mit 32 Bit lassen sich 2³² = 4294967296 verschiedene Zahlen darstellen. Die eine Hälfte davon ist kleiner als 0, die andere nicht. Damit ergibt sich ein Wertebereich von -2147483648 ... 2147483647.
Der nichtnegative Bereich erreicht eine betragsmäßig um 1 kleinere Grenze, da die 0 als erste nichtnegative Zahl gezählt wird.

Überlauf

Ein Überlauf entsteht immer dann, wenn die angegebenen Grenzen überschritten werden. Da nur 32 Bit zur Zahlenspeicherung verwendet werden, kann aber nur ein Wert im angegebenen Bereich entstehen. Überschreitet man den Wertebereich an einer Grenze, so fängt man an der anderen Grenze wieder an.
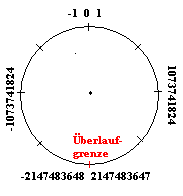
Der Wertebereich repräsentiert einen Ausschnitt aus der Zahlengeraden, also eine Strecke. Den Überlauf kann man sich vorstellen, indem man die Enden der Strecke zu einem Kreis verbindet. Eine Addition bedeutet eine Bewegung in Uhrzeigerrichtung. Eine Subtraktion bedeutet eine Bewegung gegen den Uhrzeigersinn.

0 + 1 = 1 0 - 1 = -1 2147483647 + 1 = -2147483648 //Überlauf -2147483648 - 1 = 2147483647 //Überlauf

Veranschaulichung des Überlaufs bei Dezimalzahlen

Grund für den Übergang von der Zahlengeraden zum Zahlenkreis ist der beschränkte Speicherplatz.
Angenommen, wir hätten für die Speicherung natürlicher Zahlen nur zwei Stellen zur Verfügung:

Normalerweise würde man zählen; indem man zu jeder Zahl ihren Nachfolger bestimmt.
0 → 1 → 2 →...→ 9 → 10 →...→ 99 → 100 → 101 → 102→...→ 199 → 200 → 201 → 202 →...

Da in unserem Beispiel nur zwei Stellen gespeichert werden können, gibt es für die blau markierten Hunderter keinen Speicherplatz mehr. Alles was über zwei Stellen hinaus geht, fällt weg. Dadurch entsteht folgende Zählweise:
0 → 1 → 2 →...→ 9 → 10 →...→ 99 → 00 → 01 → 02→...→ 99 → 00 → 01 → 02 →...

Wie man hier leicht sieht, ist 99 die größte darstellbare Zahl. Nach 99 geht es wieder mit 0 los, die Zählung beginnt von vorn.

Die Beschränkung auf zwei Stellen hat 2 Konsequenzen:

1. Man kann nur endlich viele Zahlen darstellen (hier von 0 bis 99).
   Damit wird aus der Zahlengeraden mit unendlich vielen Zahlen eine Zahlenstrecke mit endlich vielen Zahlen.
2. Aus der Zahlenstrecke wird ein Zahlenkreis, da bei Überschreitung des Höchstwertes wieder mit dem kleinsten Wert begonnen wird.

Darstellung nichtnegativer Zahlen im Speicher

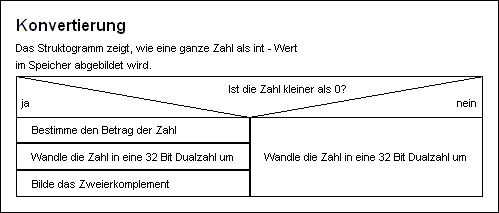
Hier wird lediglich die Dezimalzahl in eine Dualzahl umgewandelt und auf 32Bit (int-Werte belegen 4 Byte) aufgefüllt.

z.B. 12₁₀ = 1100₂ = 00000000000000000000000000001100₂

Darstellung negativer Zahlen im Speicher

Ein Minuszeichen im Speicher gibt es nicht. Da existieren nur 0 und 1. Es ist also eine Frage, wie man eine Bitdarstellung als negativen Wert interpretieren kann.
Java verwendet für die Kodierung folgende Überlegungen.

Rückführung der Subtraktion auf die Addition

Eine negative Zahl entsteht, wenn man von 0 eine positive Zahl abzieht.
z.B. -12 = 0 - 12

Die Subtraktion lässt sich auf die Addition der Komplementzahl zurück führen.
Dabei ist die Komplementzahl die Ergänzung einer Zahl zur nächsten 10er-Potenz. Bei zweistelligen Zahlen wäre das die Ergänzung zu 100.

Beispiel

     64 --> Komplementzahl = 36  (100-64)
     12 --> Komplementzahl = 88  (100-12)
   

Dann lässt sich die Subtraktion zweier Zahlen (z.B. 37 - 12) auf die Addition des Komplements zurückführen.

     

       

        
Aufgabe
        
Komplement
        
Klammern auflösen
        
Ergebnis
       
       

        
37 - 12 =
        
37 - (100-88) =
        
37 +88 -100 =
        
25 
       

     

   

In der realen Rechnung muss man nur das Komplement addieren. Durch die Beschränkung auf zwei Stellen fallen führende Stellen sowieso weg.
Verkürzt sieht die Rechnung dann so aus :

     37 - 12 = 37 +88 = 25  <-- Die Subtraktion wurde auf die Additon des Komplements zurückgeführt.
   

Ein Fehler steckt noch in den bisherigen Überlegungen. Um die Komplementzahl zu berechnen, muss die Zahl von der nächst höheren 10er-Potenz abgezogen werden, hier von 100. Diese Zahl ist aber dreistellig, kann in unserem Beispiel also nicht gespeichert werden.
Hier behilft man sich mit einem Trick.
Anstatt von 100, zieht man die Zahl von höchsten zweistelligen Zahl (also 99) ab, muss dann im Ergebnis aber noch 1 dazu addieren.
Die Berechnung der Komplementzahl ändert sich zu:

     64 --> Komplementzahl = 36  (99 + 1 - 64  bzw. 99 - 64 + 1)
     12 --> Komplementzahl = 88  (99 + 1 - 12  bzw. 99 - 12 + 1)
   

Übertragung der Gedanken auf das Dualsystem.

Die Subtraktion wird auf die Addition der Komplementzahl zurückgeführt, der Ergänzung zur nächst höheren 2er-Potenz, also eine 1 mit 32 Nullen.

      100000000000000000000000000000000
    -  00000000000000000000000000001100
    -----------------------------------
       11111111111111111111111111110100
   

Die Rechnung lautet nun
00000000000000000000000000000000₂ + 11111111111111111111111111110100₂ = 11111111111111111111111111110100₂

Und da ist wieder die kleine Nachlässigkeit. Wir haben für int-Werte nur 32 Bit zur Verfügung, benötigen für die Komplementbildung aber 33 Bit.
Wir nutzen jetzt die gleiche Überlegung wie bei den Dezimalzahlen. Wir nehmen für die Komplementbildung die höchste 32 Bit- Zahl, müssen aber dann zum Ergebnis 1 addieren.

     11111111111111111111111111111111
   - 00000000000000000000000000001100
   ----------------------------------
     11111111111111111111111111110011
   +                                1
   ----------------------------------
     11111111111111111111111111110100
   

Zusammenfassung

Für Dualzahlen bildet man das Zweierkomplement, indem man alle Bits negiert und das Ergebnis um 1 erhöht.

Das Verfahren

Übrigens: Die Bildung des Komplements ist seine eigene Umkehrfunktion. D.h., das Komplement des Komplements einer Zahl ist die Zahl selbst.

zurück Beispiel